Yerçekimi

Yer çekimi, Dünya'nın kütleçekimidir. Dünya yüzeyinde veya yakınındaki nesneleri etkiler ve onlara yer çekimi ivmesini kazandırır. Dünya yüzeyinde tüm cisimler bu ivme ile düşerler (düşen cisim denklemleri). İvmenin Paris'teki değeri tam olarak 9,80665 m/s² dir. M kütlesine sahip bir cisme doğru olan yerçekimi ivmesi


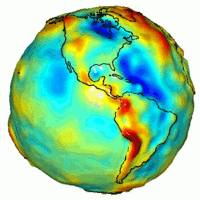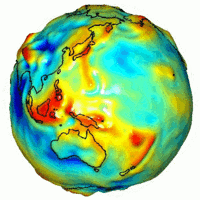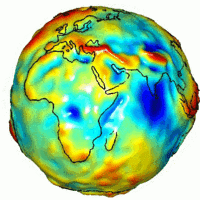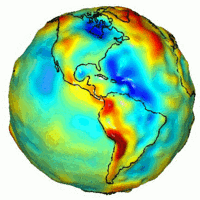
Dünyanın NASA'nın GRACE misyonunda ölçülen yerçekimi, ideal düz bir Yerküre'nin teorik çekimden farkı göstermektedir. Bu ideal şekle Dünya elipsoidi denir. Kırmızı bölgeler, çekimin idealden fazla olduğu yerleri, mâvi bölgeler de daha hafif olduğu yerlerdir.

g={MG \over r^{2}}

formülüyle hesaplanır.

Büyüklükte değişimDüzenle

Düzgün kütle yoğunluğuna sahip, dönmeyen mükemmel bir küre veya yoğunluğu yalnızca merkezden uzaklığa göre değişen (küresel simetri), üzerindeki tüm noktalarda tekdüze büyüklükte bir yerçekimi alanı oluşturacaktır. onun yüzey. Dünya dönüyor ve aynı zamanda küresel olarak simetrik de değil; daha ziyade, Ekvator'da şişkin iken kutuplarda biraz daha düzdür: bir basık sfero. Sonuç olarak, yüzeyindeki yerçekiminin büyüklüğünde küçük sapmalar vardır.

Dünya yüzeyindeki yerçekimi Peru'daki Nevado Huascarán dağındaki 9,7639 m / s ² ile Arktik Okyanusu 'nun yüzeyi.^[1] Büyük şehirlerde , aralık 9.7806'dan ^[2] Kuala Lumpur, Meksiko ve Singapur 'dan Oslo ve Helsinki' de 9.825'e.

Geleneksel değerDüzenle

1901'de üçüncü Ağırlıklar ve Ölçüler Genel Konferansı Dünya yüzeyi için standart bir yerçekimi ivmesi tanımladı: g _n = 9.80665 m / s ². 1888'de Paris yakınlarındaki Pavillon de Breteuil 'de yapılan ölçümlere dayanıyordu ve deniz seviyesinde 45 ° enlemine dönüştürmek için teorik bir düzeltme uygulandı.^[3] Bu tanım, belirli bir yerin değeri veya dikkatlice hesaplanmış bir ortalama değildir, ancak daha iyi bir gerçek yerel değer bilinmiyorsa veya önemli değilse kullanılacak bir değer için bir anlaşmadır.^[4] Ayrıca kilogram kuvvet ve pound kuvvet.

EnlemDüzenle

Dünya'nın yüzeyi dönüyor, bu nedenle eylemsiz bir referans çerçevesi değil. Ekvatora yakın enlemlerde, Dünya'nın dönüşü tarafından üretilen dışa doğru merkezkaç kuvveti kutup enlemlerinden daha büyüktür. Bu, Dünya'nın yerçekimini küçük bir dereceye kadar - Ekvator'da maksimum% 0,3'e kadar - karşı koyar ve düşen nesnelerin görünen aşağı doğru ivmesini azaltır.

Farklı enlemlerdeki yerçekimi farkının ikinci ana nedeni, Dünya'nın ekvatoral şişkinlik (kendisi de dönüşten kaynaklanan merkezkaç kuvvetinin neden olduğu) Ekvator'daki nesnelerin, kutuplardaki nesnelerden daha gezegenin merkezinden daha uzak olmasına neden olmasıdır. İki cisim (Dünya ve tartılan nesne) arasındaki yerçekiminden kaynaklanan kuvvet, aralarındaki mesafenin karesiyle ters orantılı olarak değiştiğinden, Ekvator'daki bir nesne kutuplardaki bir nesneden daha zayıf bir çekim kuvveti yaşar.

Kombinasyon halinde, ekvator çıkıntısı ve dönüş nedeniyle yüzey merkezkaç kuvvetinin etkileri, deniz seviyesindeki yerçekiminin Ekvator'da yaklaşık 9.780 m / s ² 'den yaklaşık 9.832 m / s'ye yükseldiği anlamına gelir ² kutuplarda olduğundan, bir nesne kutuplarda Ekvator'dakinden yaklaşık% 0,5 daha ağır olacaktır.^[5]^[6]

RakımDüzenle

Grafik, yüzey üzerindeki bir nesnenin yüksekliğine göre yerçekimindeki değişimi gösterir

Yerçekimi, Dünya yüzeyinin üzerine çıktıkça rakımla birlikte azalır, çünkü daha yüksek rakım, Dünya merkezinden daha büyük mesafe anlamına gelir. Diğer her şey eşit olduğunda, deniz seviyesinden rakımdaki 9.000 metre (30.000 ft) 'e yükselmesi ağırlıkta yaklaşık% 0,29 oranında azalmaya neden olur. (Görünür ağırlığı etkileyen ek bir faktör, bir nesnenin kaldırma kuvvetini azaltan rakımdaki hava yoğunluğundaki azalmadır.^[7] Bu, bir kişinin 9.000 metre yükseklikte görünen ağırlığını yaklaşık% 0,08 oranında artırmak)

Yörüngedeki astronotların ağırlıksız oldukları, çünkü Dünya'nın yerçekiminden kaçacak kadar yükseğe uçtular. Aslında, ISS 'nin tipik bir yörüngesine eşdeğer olan 400 kilometre (250 mi) yükseklikte, yerçekimi hala Dünya'nın yüzeyindekinin neredeyse% 90'ı kadar güçlü. Ağırlıksızlık aslında yörüngedeki nesneler serbest düşüş içinde olduğu için oluşur.^[8]

Zemin yüksekliğinin etkisi zeminin yoğunluğuna bağlıdır (Döşeme düzeltmesi bölümüne bakın). Deniz seviyesinden dağların üzerinden 9.100 m (30.000 ft) üzerinde uçan bir kişi, aynı yükseklikteki ama denizin üzerindeki birinden daha fazla yerçekimi hissedecektir. Bununla birlikte, Dünya yüzeyinde duran bir kişi, yükseklik daha yüksek olduğunda daha az yerçekimi hisseder.

$g h$ deniz seviyesinden $h$ yükseklikte yerçekimi ivmesidir.
$R e$ Dünyanın ortalama yarıçapı 'dır.
$g 0$ standart yerçekimi ivmesi 'dir.

Formül, Dünya'yı kütlenin radyal olarak simetrik dağılımına sahip mükemmel bir küre olarak ele alıyor; daha doğru bir matematiksel işlem aşağıda tartışılmaktadır.

DerinlikDüzenle

Ön Referans Dünya Modeline (PREM) göre Dünya'nın radyal yoğunluk dağılımı.^[9]

Ön Referans Dünya Modeline (PREM) göre dünyanın yerçekimi.^[9] Karşılaştırma için küresel simetrik bir Dünya için iki model dahil edilmiştir. Koyu yeşil düz çizgi, Dünya'nın ortalama yoğunluğuna eşit sabit bir yoğunluk içindir. Açık yeşil eğri çizgi, merkezden yüzeye doğrusal olarak azalan bir yoğunluk içindir. Merkezdeki yoğunluk, PREM'deki ile aynıdır, ancak yüzey yoğunluğu, kürenin kütlesi gerçek Dünya'nın kütlesine eşit olacak şekilde seçilir.

Dünya'nın merkezinden $r$ mesafedeki yaklaşık bir yerçekimi değeri, Dünya'nın yoğunluğunun küresel olarak simetrik olduğu varsayılarak elde edilebilir. Yerçekimi, yalnızca $r$ yarıçaplı kürenin içindeki kütleye bağlıdır. Yerçekiminin ters kare yasasından dışarıdan gelen tüm katkılar birbirini götürür. Diğer bir sonuç da, yerçekiminin, tüm kütlenin merkezde yoğunlaşması gibi aynı olmasıdır. Bu nedenle, bu yarıçaptaki yerçekimi ivmesi ^[10]

g(r)=-\ frac{GM(r)}{r^{2}}.

burada $G$ yerçekimi sabiti ve $M (r)$ , $r$ yarıçapı içindeki toplam kütledir. Dünyanın sabit bir yoğunluğu $ρ$ olsaydı, kütle $M (r) = (4/3) π ρr 'olurdu ' 3$ ve yer çekiminin derinliğe bağımlılığı

g(r)=\ frac{4\ pi}{3}G\ rhor.

$d$ derinliğindeki yerçekimi $g'$ şu şekilde verilir: $g'=' 'g' '(1 -' 'd' '/' 'R' ')$ burada $g$ yerçekimine bağlı ivmedir Dünya'nın yüzeyinde, $d$ derinliktir ve $R$ Dünya nın yarıçapıdır. Yoğunluk, merkezdeki yoğunluk $ρ 0$ 'den $' 'ρ' ' 1 </ sub >$ yüzeyde, ardından $ρ (r) = ρ 0 - (ρ < alt> 0 - ρ 1) r / r e$ ve bağımlılık

g(r)=\ frac{4\ pi}{3}G\ rho_{0}r-\ piG\ left(\ rho_{0}-\ rho_{1}\ right)\ frac{r^{2}}{r_{\ mathrm{e}}}.

Sismik seyahat sürelerinden (Adams – Williamson denklemi çıkarılan) yoğunluk ve yerçekiminin gerçek derinlik bağımlılığı aşağıdaki grafiklerde gösterilmektedir.

Yerel topografya ve jeolojiDüzenle

Şablon:Ayrıca bkz. Topografya (dağların varlığı gibi), jeoloji (civardaki kayaların yoğunluğu gibi) ve daha derin tektonik yapı bölgelerindeki yerel farklılıklar yerel ve bölgesel farklılıklara neden olur yerçekimi anormallikleri olarak bilinen yerçekimi alanında.^[11] Bu anormalliklerden bazıları çok kapsamlı olabilir, bu da deniz seviyesinde şişkinliklere ve sarkaç saatlerin senkronizasyondan çıkmasına neden olabilir .

Bu anomalilerin incelenmesi, yerçekimsel jeofizik temelini oluşturur. Dalgalanmalar oldukça hassas gravimetre lerle ölçülür, topografyanın etkisi ve diğer bilinen faktörlerin etkisi çıkarılır ve elde edilen verilerden sonuçlar çıkarılır. Bu tür teknikler artık araştırmacılar tarafından petrol ve maden yatakları nı bulmak için kullanılmaktadır. Daha yoğun kayaçlar (genellikle mineral cevher içerirler), Dünya yüzeyinde normalden daha yüksek yerel yerçekimi alanlarına neden olur. Daha az yoğun tortul kaya tam tersine neden olur.

Diğer faktörlerDüzenle

Havada veya suda nesneler, görünen yerçekimi kuvvetini azaltan (bir nesnenin ağırlığı ile ölçüldüğü üzere) destekleyici bir kaldırma kuvveti kuvvetine maruz kalır. Etkinin büyüklüğü sırasıyla hava yoğunluğuna (ve dolayısıyla hava basıncına) veya su yoğunluğuna bağlıdır; ayrıntılar için Görünen ağırlık bölümüne bakın.

Ay ve Güneş 'in yerçekimi etkileri (aynı zamanda gelgitler' lerin nedeni), göreli konumlarına bağlı olarak, Dünya'nın yerçekiminin görünen gücü üzerinde çok küçük bir etkiye sahiptir; tipik varyasyonlar bir gün boyunca 2 µm / s ² (0.2 mGal) şeklindedir.

KaynakçaDüzenle

^ Hirt, Christian; Claessens, Sten; Fecher, Thomas; Kuhn, Michael; Pail, Roland; Rexer, Moritz (28 Ağustos 2013). "Dünyanın yerçekimi alanının yeni ultra yüksek çözünürlüklü resmi". Jeofizik Araştırma Mektupları. 40 (16): 4279-4283. Bibcode:2013GeoRL..40.4279H.
^ ""Wolfram | Alpha Gravity in Kuala Lumpur", Wolfram Alpha, Kasım 2020'de erişildi". 1 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 19 Haziran 2021.
^ Terry Quinn (2011). From Atomlardaki Artefaktlar: BIPM ve Nihai Ölçüm Standartları Arayışı. Oxford University Press. s. 127. ISBN 978-0-19-530786-3.
^ 3. CGPM'nin Çözümü (1901), sayfa 70 (cm / s ² cinsinden). BIPM - 3. CGPM'nin Çözünürlüğü 14 Mayıs 2013 tarihinde Wayback Machine sitesinde arşivlendi.
^ Boynton, Richard (2001). " Hassas Kütle Ölçümü " (PDF). Sawe Kağıt No. 3147. Arlington, Teksas: S.A.W.E., Inc. Erişim tarihi: 21 Ocak 2007.
^ "Astronomi Hakkında Meraklı?" 17 Ocak 2015 tarihinde Wayback Machine sitesinde arşivlendi., Cornell Üniversitesi, Haziran 2007'de alındı
^ ne zaman-bir-dağ-ama-ben-(sss-kütle-ve-yoğunluk) "Dağın tepesinde kendimi 'daha hafif' hissediyorum ama öyle miyim?", Ulusal Fizik Laboratuvarı SSS
^ "The G's in Makine " 21 Eylül 2020 tarihinde Wayback Machine sitesinde arşivlendi., NASA, bkz." Editörün 2. notu "
^ ^a ^b A. M. Dziewonski, DL Anderson (1981). "Ön referans Dünya modeli" (PDF). Dünya Fiziği ve Gezegen İç Mekanları. 25 (4): 297-356. ^{[ölü/kırık bağlantı]}
^ Tipler, Paul A. (1999). Bilim adamları ve mühendisler için fizik (4th bas.). New York: W.H. Freeman / Worth Yayıncıları. ss. 336-337. ISBN 9781572594913.
^ Watt, A. B.; Daly, S. F. (Mayıs 1981). "Uzun dalga boyu yerçekimi ve topografya anormallikleri". Yeryüzü ve Gezegen Bilimlerinin Yıllık İncelemesi. 9: 415-418.

Fizik ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz.

[1] Hirt, Christian; Claessens, Sten; Fecher, Thomas; Kuhn, Michael; Pail, Roland; Rexer, Moritz (28 Ağustos 2013). "Dünyanın yerçekimi alanının yeni ultra yüksek çözünürlüklü resmi". Jeofizik Araştırma Mektupları. 40 (16): 4279-4283. Bibcode:2013GeoRL..40.4279H.

[Wolfram_Alpha-2] ""Wolfram | Alpha Gravity in Kuala Lumpur", Wolfram Alpha, Kasım 2020'de erişildi". 1 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 19 Haziran 2021.

[3] Terry Quinn (2011). From Atomlardaki Artefaktlar: BIPM ve Nihai Ölçüm Standartları Arayışı. Oxford University Press. s. 127. ISBN 978-0-19-530786-3.

[4] 3. CGPM'nin Çözümü (1901), sayfa 70 (cm / s ² cinsinden). BIPM - 3. CGPM'nin Çözünürlüğü 14 Mayıs 2013 tarihinde Wayback Machine sitesinde arşivlendi.

[Boynton-5] Boynton, Richard (2001). " Hassas Kütle Ölçümü " (PDF). Sawe Kağıt No. 3147. Arlington, Teksas: S.A.W.E., Inc. Erişim tarihi: 21 Ocak 2007.

[6] "Astronomi Hakkında Meraklı?" 17 Ocak 2015 tarihinde Wayback Machine sitesinde arşivlendi., Cornell Üniversitesi, Haziran 2007'de alındı

[7] zaman-bir-dağ-ama-ben-(sss-kütle-ve-yoğunluk) "Dağın tepesinde kendimi 'daha hafif' hissediyorum ama öyle miyim?", Ulusal Fizik Laboratuvarı SSS

[8] "The G's in Makine " 21 Eylül 2020 tarihinde Wayback Machine sitesinde arşivlendi., NASA, bkz." Editörün 2. notu "

[prem-9] A. M. Dziewonski, DL Anderson (1981). "Ön referans Dünya modeli" (PDF). Dünya Fiziği ve Gezegen İç Mekanları. 25 (4): 297-356. ^{[ölü/kırık bağlantı]}

[10] Tipler, Paul A. (1999). Bilim adamları ve mühendisler için fizik (4th bas.). New York: W.H. Freeman / Worth Yayıncıları. ss. 336-337. ISBN 9781572594913.

[11] Watt, A. B.; Daly, S. F. (Mayıs 1981). "Uzun dalga boyu yerçekimi ve topografya anormallikleri". Yeryüzü ve Gezegen Bilimlerinin Yıllık İncelemesi. 9: 415-418.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]