Logistik dağılım
Olasılık kuramı ve istatistik bilim kollarında, logistik dağılım bir sürekli olasılık dağılımdır. Logistik dağılımın yığmalı dağılım fonksiyon bir logistik fonksiyondur ve bu fonksiyon logistik regresyon ve ileriye-geçiş-sağlayan sinirsel ağlar konularında da rol oynar.
Olasılık yoğunluk fonksiyonu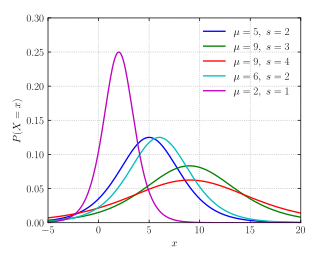
| |
Yığmalı dağılım fonksiyonu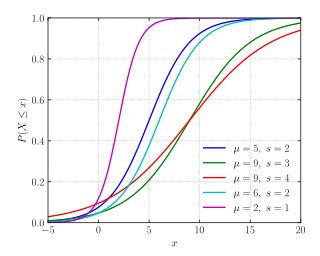
| |
| Parametreler | konum (reel) ölçe (reel) |
|---|---|
| Destek | |
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | for , beta fonksiyonu |
| Karakteristik fonksiyon | for |
Şekil bakımından çan şeklinde olan normal dağılıma çok benzer; fakat kuyrukları daha ağır olduğu için daha basık bir şekil gösterir.
Tanımlama
değiştirYığmalı dağılım fonksiyonu
değiştirLogistik dağılım ismini yığmalı dağılım fonksiyonuna atıfla alır çünkü bu fonksiyon matematiksel logistik fonksiyonlar ailesinin bir üyesidir:
Olasılık yoğunluk fonksiyonu
değiştirLogistik dağılım için olasılık yoğunluk fonksiyonu (OYF) şu formülle ifade edilir:
OYF bir hiperbolik sekant fonksiyonunun karesi şeklinde olduğu görülür.
Kuantil fonksiyonu
değiştirLogistik fonksiyon için ters yığmalı dağılım fonksiyonu logit fonksiyonunun bir genelleştirilmesi suretiyle olarak elde edilir ve bu da şöyle tanımlanır:
Alternatif şekilde parametreleme
değiştirLogistik dağılım için bir alternatif parametreleme eşitliği kullanarak terimlerin değiştirilmesi suretiyle elde edilebilir. Böylece logistik dağılım için yoğunluk fonskiyonu şöyle değişik şekilde ifade edilebilir:
Uygulamalar
değiştirMilletlerarası satranç federasyonu FIDE ve bunun üyesi olan birçok milli satranç federasyonu satranç oyuncularının sınıflandırılması için kullanılan formüllerde logistik dağılım kullanmaya başlamışlardır.
İlişkili dağılımlar
değiştirEğer X bir logistik fonksiyona göre dağılım gösteriyorsa log(X) bir log-logistik dağılım şeklindedir ve log(X - a) bir kaydırılmış log-logistik dağılım gösterir.
Kaynakça
değiştirBalakrishnan, N. (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. ISBN 0-8247-8587-8.
Johnson,, N.L. (1995). Continuous Univariate Distributions Vol.2. Marcel Dekker, New York. ISBN 0-471-58494-0.
İçsel kaynaklar
değiştir- Vikipedi:en:Logistic distribution İngilizce Vikipedia Logistic distribution maddesi
- logistik regresyon
- sigma şekilli fonksiyon












