Ki-kare dağılımı

Olasılık kuramı ve istatistik bilim dallarında ki-kare dağılım (x² dağılımı) özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur.

ki-kare

Olasılık yoğunluk fonksiyonu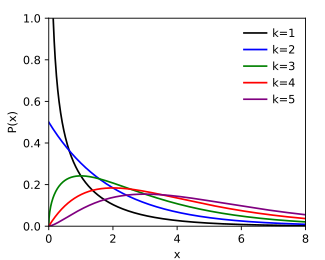
Yığmalı dağılım fonksiyonu
Parametreler	$k>0\,$ serbestlik derecesi
Destek	$x\in [0;+\infty )\,$
Olasılık yoğunluk fonksiyonu (OYF)	${\frac {(1/2)^{k/2}}{\Gamma (k/2)}}x^{k/2-1}e^{-x/2}\,$
Birikimli dağılım fonksiyonu (YDF)	${\frac {\gamma (k/2,x/2)}{\Gamma (k/2)}}\,$
Ortalama	$k\,$
Medyan	yaklaşık olarak $k-2/3\,$
Mod	$k-2\,$ eğer $k\geq 2\,$
Varyans	$2\,k\,$
Çarpıklık	${\sqrt {8/k}}\,$
Fazladan basıklık	$12/k\,$
Entropi	${\frac {k}{2}}\!+\!\ln(2\Gamma (k/2))\!+\!(1\!-\!k/2)\psi (k/2)$
Moment üreten fonksiyon (mf)	$(1-2\,t)^{-k/2}$ eğer $2\,t<1\,$
Karakteristik fonksiyon	$(1-2\,i\,t)^{-k/2}\,$

Bu dağılım, gamma dağılımından elde edilir.

x, $\lambda$ ve n parametreleri ile gamma dağılımına sahip olsun:

$f(x)={\frac {1}{\lambda ^{n}\Gamma (n)}}x^{n-1}e^{-{\frac {x}{\lambda }}}\qquad ,x>0$ olur.

Burada $\lambda =2$ ve $n=\nu /2$ alınırsa, elde edilen yeni dağılıma, $\nu$ serbestlik derecesiyle ki-kare dağılımı denir ve $\mathrm {X} _{\nu }^{2}$ ile gösterilir.

x, $\nu$ serbestlik derecesiyle ki-kare dağılımına sahip ise:

ki-kare 1 n(0.1)'e eşittir $f(x)={\frac {1}{2^{\frac {\nu }{2}}\Gamma ({\frac {\nu }{2}})}}x^{{\frac {\nu }{2}}-1}e^{-x/2}\qquad ,x>0$ olur.

Teorem 1

$x\sim N(0,1)$ ise $x^{2}\sim \mathrm {X} _{1}^{2}$ olur.

Teorem 2

$x_{1},x_{2},\cdots ,x_{n}$ rassal değişkenler N(0,1) dağılımına sahip olsun.

$y=\sum _{i=1}^{n}x_{i}^{2}$ ise $y\sim \mathrm {X} _{n}^{2}$ olur.

Teorem 3

$\sigma ^{2}$ varyansı bilinen, $N(\mu ,\sigma ^{2})$ dağılımına sahip rastgele örneklem $x_{1},x_{2},\cdots ,x_{n}$ ve $s^{2}$ örneklem varyansı olmak üzere:
${\frac {(n-1)s^{2}}{\sigma ^{2}}}\sim \mathrm {X} _{n-1}^{2}$ olur.

Karakteristikleri

Olasılık yoğunluk fonksiyonu

Ki-kare dağılım için olasılık yoğunluk fonksiyonu şu olur:

$f(x;k)={\begin{cases}\displaystyle {\frac {1}{2^{k/2}\Gamma (k/2)}}\,x^{(k/2)-1}e^{-x/2}&{\text{eğer }}x>0,\\0&{\text{eğer }}x\leq 0,\end{cases}}$

Burada $\Gamma$ bir Gamma fonksiyonu bulunduğunu gösterir ve bu yarım-tamsayılar için özel değerler gösterir.

Yığmalı dağılım fonksiyonu

Ki-kare dağılımının yığmalı dağılım fonksiyonu şudur:

$F(x;k)={\frac {\gamma (k/2,x/2)}{\Gamma (k/2)}}=P(k/2,x/2)$

burada $\gamma (k,z)$ aşağı kısmı tamamlanmamış Gamma fonksiyonu ve $P(k,z)$ ise tanzim edilmiş Gamma fonksiyonu olur.

Ki-karenin için verilen tablolar (biri aşağıda verilmiştir) yığmalı dağılim fonksiyonundan elde edilmektedir. Bu tablolar birçok değişik kaynaklardan bulunabilir. Örneğin bu fonksiyon için tablolar spreadsheet ve istatistik program paketlerinde bulunmaktadır.

Karakteristik fonksiyonu

Ki-kare dağılımının karakteristik fonksiyonu şöyle yazılır:

$\chi (t;k)=(1-2it)^{-k/2}.\,$

Özellikleri

• Ki-kare dağılımı cikarimsal istatistik analizde epeyce kullanış alanı bulmuştur. Parametrik istatistik olarak varyans değeri güvenlik aralığı ve hipotez testi, parametrik olamayan uygunluk iyiliği testi, olumsallık tablosu üzerinde bağımsızlık testi ve ki-kareye bağlı ortaklılık katsayıları, uzaklık ölçüleri vb.
• Varyanslar analizinde F-dagiliminin iki ki-kare dağılımının oranından ortaya çıkması dolayışıyla önemli rol oynamaktadır.

Normal yaklaşım

Eğer $X\sim \chi _{k}^{2}$ ise, limitte $k$ sonsuzluğa yaklaştıkça $X$ normal dağılıma yaklaşır. Ancak bu eğilim (çarpıklık ${\sqrt {8/k}}$ ve basıklık fazlalığı $12/k$ olduğundan dolayı) yavaş gelişmektedir. Ki-kare dağılımının iki değişik dönüşüm fonksiyonu normalliğe çok daha hızla yaklaşma göstermektedir:

Fisher ispat etmiştir ki ${\sqrt {2X}}$ ifadesi, yaklaşık olarak ortalaması ${\sqrt {2k-1}}$ olan ve varyans değeri 1 olan bir normal dağılım gösterir.

Aynı normal yaklaşım sonucuna moment karşılaştırması yapılarak da erişilebilir. Bunu görmek için ki-dağılım gösteren rassal değişken $z={\sqrt {X}}$in ortalaması ve varyansı izlensin. Bunlar sırasıyla şöyle verilir:

$\mu _{z}={\sqrt {2}}{\frac {\Gamma \left(k/2+1/2\right)}{\Gamma \left(k/2\right)}}$

ve

$\sigma _{z}^{2}=k-\mu _{z}^{2}$

Burada $\Gamma (\cdot )$ bir Gamma fonksiyonudur. $\mu _{z}$ ifadeli gamma fonksiyonunun özel oranı (particular ratio) şu seri halinde açılabilir:

${\frac {\Gamma \left(N+1/2\right)}{\Gamma \left(N\right)}}={\sqrt {N}}\left(1-{\frac {1}{8N}}+{\frac {1}{128N^{2}}}+{\frac {5}{1024N^{3}}}-{\frac {21}{32768N^{4}}}+\ldots \right).$

$N\gg 1$ olduğu halde bu oran için şöyle yaklaşım bulunur: ${\frac {\Gamma \left(N+1/2\right)}{\Gamma \left(N\right)}}\approx {\sqrt {N}}\left(1-{\frac {1}{8N}}\right)\approx {\sqrt {N}}\left(1-{\frac {1}{4N}}\right)^{0.5}={\sqrt {N-1/4}}.$

Sonra basitleşen moment karşılaştırılması sonuçları şu yaklaşık $z$ dağılımı verirler;

$z\sim {\mathcal {N}}\left({\sqrt {k-1/2}},{\frac {1}{2}}\right)$,

Bundan da şu ifade hemen çıkartılabilir\:

${\sqrt {2X}}\sim {\mathcal {N}}\left({\sqrt {2k-1}},1\right)$.

Wilson ve Hilferty [1931] göstermiştir ki ${\sqrt[{3}]{X/k}}$ ifadesi, ortalaması $1-2/(9k)$ ve varyansı $2/(9k)$ olan bir normal dağılıma yaklaşıktır.

$k$ serbestlik derecesi olan bir ki-kare dağılımı gösteren bir rassal değişken için beklenen değer $k$ olur. Aynı dağılımın medyan değeri yaklaşık olarak şu ifade ile verilir:

$k-{\frac {2}{3}}+{\frac {4}{27k}}-{\frac {8}{729k^{2}}}.$

Eğer serbestlik derecesi 2 ise üstel dağılım ile aynı dağılımdır.

Enformasyon entropisi

Enformasyon entropisi ifadesi şöyle verilir:

$H=\int _{-\infty }^{\infty }f(x;k)\ln(f(x;k))dx={\frac {k}{2}}+\ln \left(2\Gamma \left({\frac {k}{2}}\right)\right)+\left(1-{\frac {k}{2}}\right)\psi (k/2).$

Burada $\psi (x)$ bir Digamma fonksiyonudur.

İlişkili dağılımlar

• Serbestlik derecesi 2ye eşit olan $X\sim \chi _{2}^{2}$ için $X\sim \operatorname {Ustel} \left(\lambda ={\tfrac {1}{2}}\right)$ bir üstel dağılım olur.

• Normal dağılım gösteren ve birbirinden bağımsız olan $X_{i}\sim N(0,1)$ değişkenleri için $Y=\sum _{m=1}^{k}X_{m}^{2}$ ise, $Y\sim \chi _{k}^{2}$ bir ki-kare dağılımı gösterir.
• Eğer $X_{i}\sim N(\mu _{i},1)$ dağılımlarının sıfır olmayan ortalamaları varsa, o halde $Y=\sum _{m=1}^{k}X_{m}^{2}$ bir merkezsel olmayan ki-kare dağılımndan çıkartılmıştır.
• $X\sim \operatorname {Gamma} \left({\tfrac {\nu }{2}},2\right)$ olduğundan dolayı, ki-kare dağılımı $X\sim \chi _{\nu }^{2}$ bir gamma dağılımının özel halidir.
• Eğer verilmiş serbestlik dereceleri ile $X_{1}\sim \chi _{\nu _{1}}^{2}$ ve $X_{2}\sim \chi _{\nu _{2}}^{2}$ birbirinden bağımsız iken $Y={\frac {X_{1}/\nu _{1}}{X_{2}/\nu _{2}}}$ ise, $Y\sim \mathrm {F} (\nu _{1},\nu _{2})$ bir F-dağılımı gösterir.
• $Y=\sum _{m=1}^{N}X_{m}$ ifadesi için $X_{m}\sim \chi ^{2}(\nu _{m})$ değişkenleri bağımsız ve ${\bar {\nu }}=\sum _{m=1}^{N}\nu _{m}$ ise, o halde $Y\sim \chi ^{2}({\bar {\nu }})$ ifadesi bir ki-kare dağılımı gösterir.
• Eğer $X$ ki-kare dağılımı gösterirse, o halde ${\sqrt {X}}$ ifadesi de ki-kare dağılımı gösterir.
• Özellikle, eğer $X\sim \chi _{2}^{2}$ (yani 2 serbestlik derecesi gösteren ki-kare ise), o halde ${\sqrt {X}}$ ifadesi Rayleigh dağılımı gösterir.
• Eğer $X_{1},\dots ,X_{n}$ bağımsiz ama aynı dağılımlı, yani hepsi $N(\mu ,\sigma ^{2})$ normal dağılım gösteren, rassal değişkenlerse, o halde

$\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}\sim \sigma ^{2}\chi _{n-1}^{2}$

olur; burada ${\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$ dir.

• Eğer $X\sim \operatorname {CarpikLogistik} \left({\tfrac {1}{2}}\right)\,$, ise, o halde $\log(1+e^{-X})\sim \chi _{2}^{2}\,$ olur.

Çeşitli ki ve ki-kare dağılımları

İsim	İstatistik
Ki-kare dağılımı	$\sum _{i=1}^{k}{\frac {\left(X_{i}-\mu _{i}\right)^{2}}{\sigma _{i}^{2}}}$
Merkezsel olmayan ki-kare dağılımı	$\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}$
Ki dağılımı	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}$
Merkezsel olmayan ki dağılımı	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}$

Ki kare kritik değerler tablosu

g serbestlik derecesi için yukarı kuyruk alanının (olasılığın) α olmasına karşıt olan ki² kritik değeri

+-----+-----------------------------------------------------------------------+
| \  α|                                                                       |
|  \  | 0.995  0.91   0.925  0.95   0.90   0.10   0.05   0.025  0.01   0.005  |
|g  \ |                                                                       |
+-----+-----------------------------------------------------------------------+
|  1  |  0.00   0.00   0.00   0.00   0.02   2.71   3.84   5.02   6.63   7.88  |
|  2  |  0.01   0.02   0.05   0.10   0.21   4.61   5.99   7.38   9.21  10.60  |
|  3  |  0.07   0.11   0.22   0.35   0.58   6.25   7.81   9.35  11.34  12.84  |
|  4  |  0.21   0.30   0.48   0.71   1.06   7.78   9.49  11.14  13.28  14.86  |
|  5  |  0.41   0.55   0.83   1.15   1.61   9.24  11.07  12.83  15.09  16.75  |
|  6  |  0.68   0.87   1.24   1.64   2.20  10.64  12.59  14.45  16.81  18.55  |
|  7  |  0.99   1.24   1.69   2.17   2.83  12.02  14.07  16.01  18.48  20.28  |
|  8  |  1.34   1.65   2.18   2.73   3.49  13.36  15.51  17.53  20.09  21.95  |
|  9  |  1.73   2.09   2.70   3.33   4.17  14.68  16.92  19.02  21.67  23.59  |
| 10  |  2.16   2.56   3.25   3.94   4.87  15.99  18.31  20.48  23.21  25.19  |
| 11  |  2.60   3.05   3.82   4.57   5.58  17.28  19.68  21.92  24.72  26.76  |
| 12  |  3.07   3.57   4.40   5.23   6.30  18.55  21.03  23.34  26.22  28.30  |
| 13  |  3.57   4.11   5.01   5.89   7.04  19.81  22.36  24.74  27.69  29.82  |
| 14  |  4.07   4.66   5.63   6.57   7.79  21.06  23.68  26.12  29.14  31.32  |
| 15  |  4.60   5.23   6.26   7.26   8.55  22.31  25.00  27.49  30.58  32.80  |
| 16  |  5.14   5.81   6.91   7.96   9.31  23.54  26.30  28.85  32.00  34.27  |
| 17  |  5.70   6.41   7.56   8.67  10.09  24.77  27.59  30.19  33.41  35.72  |
| 18  |  6.26   7.01   8.23   9.39  10.86  25.99  28.87  31.53  34.81  37.16  |
| 19  |  6.84   7.63   8.91  10.12  11.65  27.20  30.14  32.85  36.19  38.58  |
| 20  |  7.43   8.26   9.59  10.85  12.44  28.41  31.41  34.17  37.57  40.00  |
| 21  |  8.03   8.90  10.28  11.59  13.24  29.62  32.67  35.48  38.93  41.40  |
| 22  |  8.64   9.54  10.98  12.34  14.04  30.81  33.92  36.78  40.29  42.80  |
| 23  |  9.26  10.20  11.69  13.09  14.85  32.01  35.17  38.08  41.64  44.18  |
| 24  |  9.89  10.86  12.40  13.85  15.66  33.20  36.42  39.36  42.98  45.56  |
| 25  | 10.52  11.52  13.12  14.61  16.47  34.38  37.65  40.65  44.31  46.93  |
| 26  | 11.16  12.20  13.84  15.38  17.29  35.56  38.89  41.92  45.64  48.29  |
| 27  | 11.81  12.88  14.57  16.15  18.11  36.74  40.11  43.19  46.96  49.64  |
| 28  | 12.46  13.56  15.31  16.93  18.94  37.92  41.34  44.46  48.28  50.99  |
| 29  | 13.12  14.26  16.05  17.71  19.77  39.09  42.56  45.72  49.59  52.34  |
| 30  | 13.79  14.95  16.79  18.49  20.60  40.26  43.77  46.98  50.89  53.67  |
+-----+-----------------------------------------------------------------------+

Kaynak: Kritik değerler İtalyanca Wikipedia için R (software) serbest programının qchisq(,1:30) fonksiyonu kullanılarak bulunmuştur.

Serbestlik derecesi g>30 olursa kritik değerleri bulmak için şu ifadeyi kullanmak yeterli olacaktır.

χ²_α,g = 1/2 ( z_α + √(2g-1) )²

Burada z_α Standart Normal N(0,1) için kritik değerdir (örneğin z_0,95 = 1,645 olur.)

Ayrıca bakınız

• Cochran'in teoremi
• Ters-ki-kare dağılımı
• Serbestlik derecesi (istatistik)
• Bağımsız sınamaları birleştirmek için Fisher'in yöntemi
• Merkezsel olmayan ki-kare dağılımı

Dış bağlantılar

• Ki-kare uyum-iyiliği sınaması ders notları 3 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.

Yale University Stats 101 kodlu ders için ornekler hipotez sinamasi ve parametre tahminleri konularini kapsar.

• Ki-kare kritik değerleri için On-line hesaplayıcı, Vassar College Richard Lowry'nin istatistik web sitesinde.
• Dağılımlar hesaplayıcısı29 Ocak 2007 tarihinde Wayback Machine sitesinde arşivlendi. Normal, Student'in t, ki-kare ve F dağılımları için olasılıkları ve kritik değerleri hesaplar.
• Ki-kare kritik değerleri için Ki-kare hesaplayıcısı 24 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi. South Carolina Universitesi'nde R.Webster West'in Java applet deposunda
• GraphPad tarafından hazırlanmış Ki-kare hesaplayıcısı 3 Aralık 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• Ki-kare dağılımı için tablo 3 Aralık 2007 tarihinde Wayback Machine sitesinde arşivlendi.